做了一个目标检测相关的实验, 在昆虫检测训练集上统计真实框与其匹配的锚框之间的关系, 直观解释了 Faster RCNN 中真实框编码方式的合理性.
直接看测试结果, 图形中 $x_{gt}, y_{gt}, w_{gt}, h_{gt}$ 分别表示真实框的中心坐标和宽高; $x_{a}, y_{a}, w_{a}, h_{a}$ 分别表示真实框匹配的锚框的中心坐标和宽高.
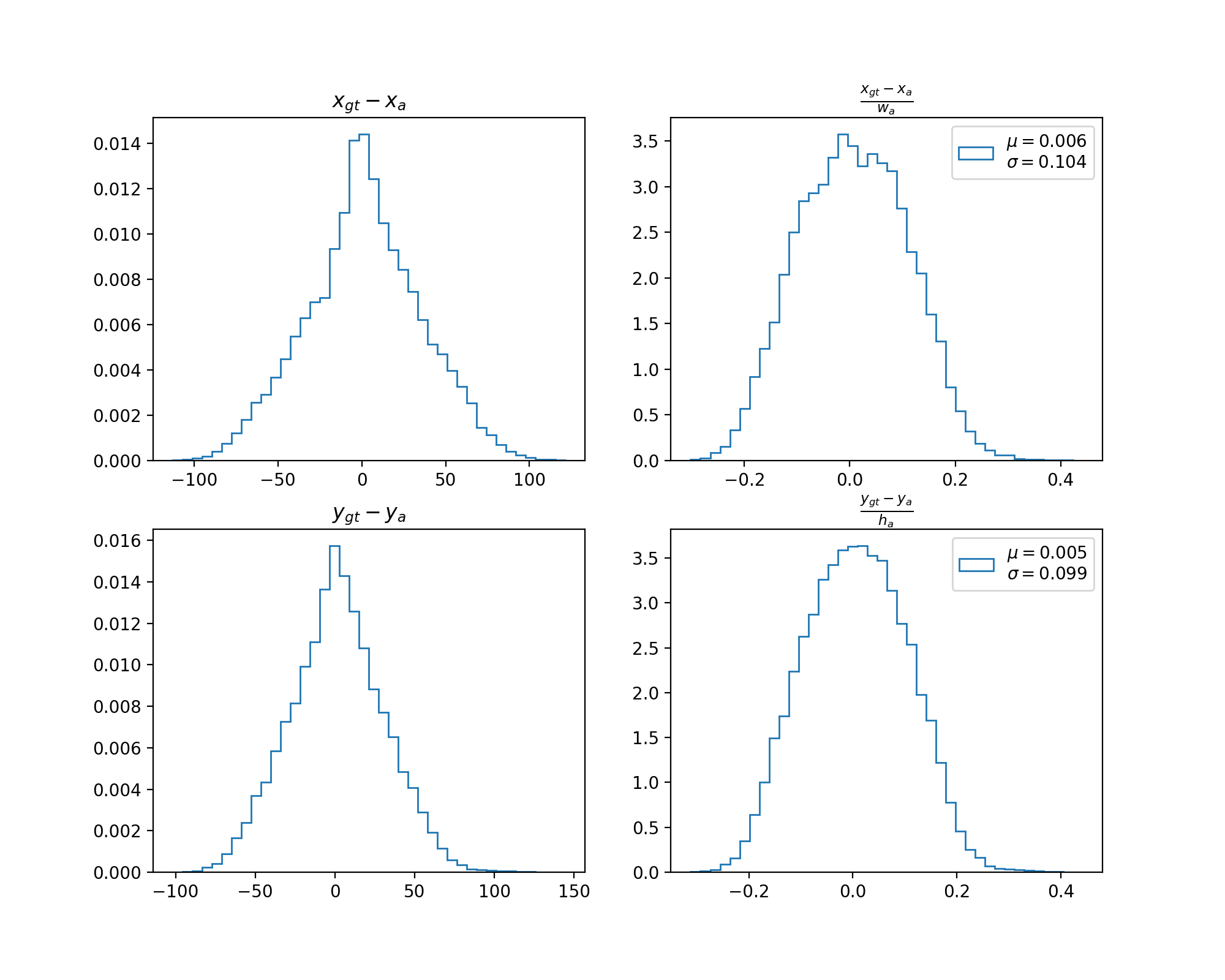
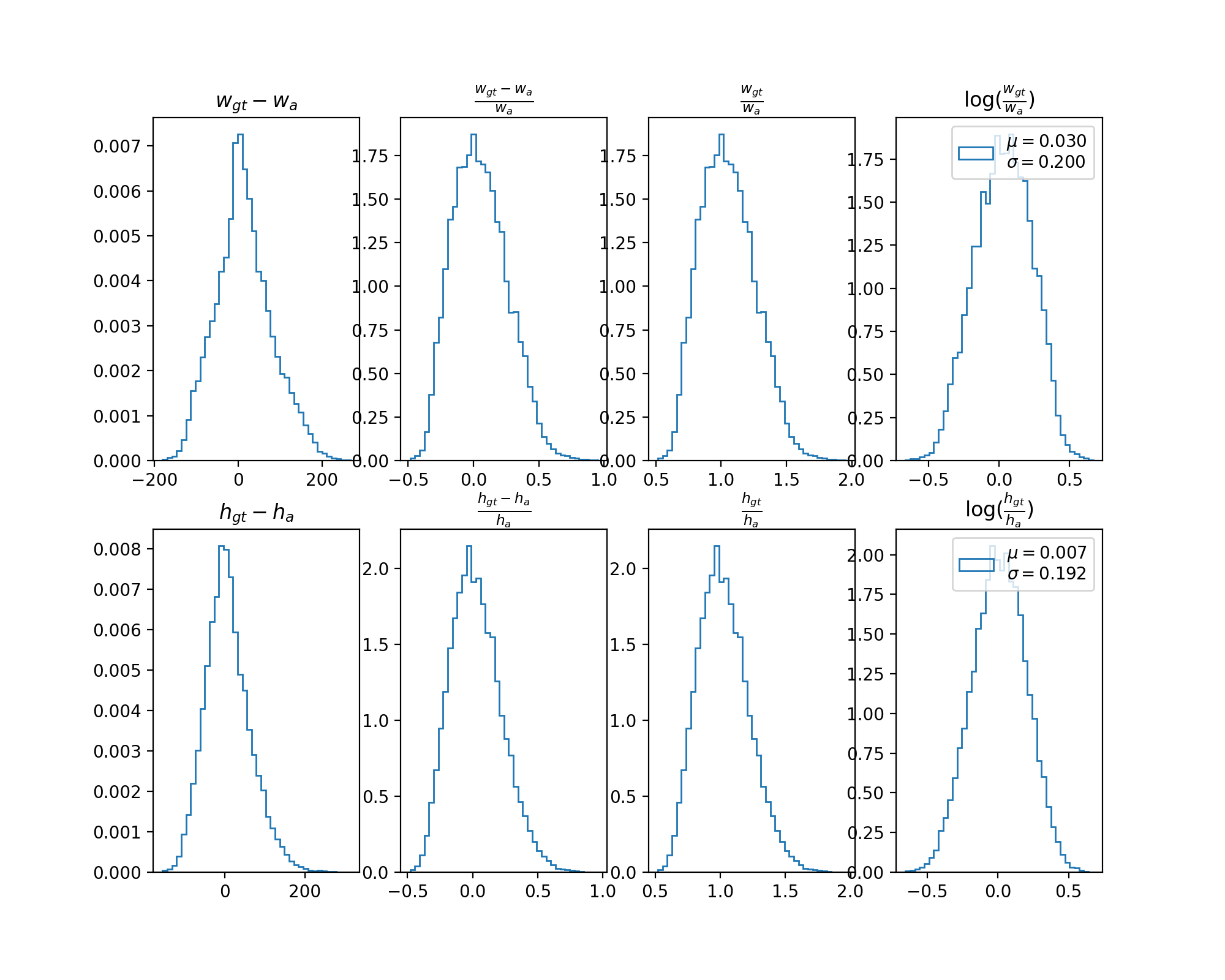
下面是观察上述两图得到的一些现象 (为了行文简单, 下面的叙述只针对中心横坐标和宽, 中心纵坐标和高有类似的结论):
1) $x_{gt} - x_a$ 和 $\frac{x_{gt} - x_a}{w_a}$ 的直方图接近均值为 0 的正态分布.
2) $w_{gt} - w_a$ 和 $\log\frac{w_{gt}}{w_a}$ 的直方图接近均值为 0 的正态分布.
3) $\frac{w_{gt} - w_a}{w_a}$ 和 $\frac{w_{gt}}{w_a}$ 的直方图左右明显不对称.
下面是基于实验现象的一些个人猜测:
1) 使用 $\frac{x_{gt} - x_a}{w_a}$ 而不是 $x_{gt} - x_a$ 来对 $x_{gt}$ 进行编码的原因是前者具有尺度不变性.
2) $\frac{w_{gt} - w_a}{w_a}$ 和 $\frac{w_{gt}}{w_a}$ 的直方图左右明显不对称, 与正态分布不相符, 所以均不选来对 $w_{gt}$ 进行编码.
3) 使用 $\log\frac{w_{gt}}{w_a}$ 而不是 $w_{gt} - w_a$ 来对 $w_{gt}$ 进行编码的原因是前者具有尺度不变性.
4) $\frac{x_{gt} - x_a}{x_a}$ 和 $\log\frac{w_{gt}}{w_a}$ 的分布的标准差并不相同, 而一般的定位 loss 是无差别的优化中心坐标和宽高的, 所以最好将两者的分布变成一样. 由此可以解释一些代码实现中为何要对编码后的中心和宽高除以一个数 (中心坐标和宽高一般对应不同的值). Bounding-Box-Encoding-Decoding 提到对编码后的中心和宽高进行归一化, 即除以统计的标准差, 个人认为要不要进行归一化与定位 loss 的类型有关 (个人观点如果是 L1 和 L2 Loss, 无需进行归一化, 如果是 Smooth L1 Loss, 最好进行归一化).
另外值得一提的是: 代码实现中通常对编码后的中心/宽高除以 0.1/0.2, 而本次实验统计出来的中心坐标/宽高的标准差也恰好在 0.1/0.2 左右. 不知道是不是巧合, 还是有更深层次的原因.
上面只是个人的一些猜测, 没有充分验证, 欢迎讨论.
更新记录
- 20211014, 发布
版权声明
保持署名-非商业用途-非衍生, 知识共享3.0协议.