在 C/C++ 中, 直接利用 (x + y) >> 1 来计算 $\left\lfloor {\left( {x + y} \right)/2} \right\rfloor$ (两个整数的平均值并向下取整)以及直接利用 (x + y + 1) >> 1 来计算 $\left\lceil {\left( {x + y} \right)/2} \right\rceil$ (两个整数的平均值并向上取整)的结果可能有误, 因为 (x + y) >> 1 和 (x + y + 1) >> 1 中的 x + y 可能会发生数值溢出. 而 $\left\lfloor {\left( {x + y} \right)/2} \right\rfloor$ 和 $\left\lceil {\left( {x + y} \right)/2} \right\rceil$ 的结果是不可能数值溢出的, 这就引发我们思考可不可能通过某种方式来规避平均值计算中的数值溢出.
注: 本文假设符号数的右移运算符进行的是算术右移, 符号数的编码方式采用的是 two's complement 编码.
方式一
利用如下公式
$$\begin{aligned} \left\lfloor {\left( {x + y} \right)/2} \right\rfloor = \left\lfloor {x/2} \right\rfloor + \left\lfloor {y/2} \right\rfloor + \left\lfloor {\left( {x\bmod 2 + y\bmod 2} \right)/2} \right\rfloor \\ \left\lceil {\left( {x + y} \right)/2} \right\rceil = \left\lfloor {x/2} \right\rfloor + \left\lfloor {y/2} \right\rfloor + \left\lceil {\left( {x\bmod 2 + y\bmod 2} \right)/2} \right\rceil \\ \end{aligned}$$
下面是对上述两式的证明:
$$\begin{aligned} \left\lfloor {\left( {x + y} \right)/2} \right\rfloor &= \left\{ {\begin{matrix} {m + n}&{x = 2m,y = 2n} \\ {m + n}&{x = 2m + 1,y = 2n} \\ {m + n}&{x = 2m,y = 2n + 1} \\ {m + n + 1}&{x = 2m + 1,y = 2n + 1} \end{matrix}} \right. \\ &= \left\lfloor {x/2} \right\rfloor + \left\lfloor {y/2} \right\rfloor + \left\lfloor {\left( {x\bmod 2 + y\bmod 2} \right)/2} \right\rfloor \\ \end{aligned}$$
$$\begin{aligned} \left\lceil {\left( {x + y} \right)/2} \right\rceil &= \left\{ {\begin{matrix} {m + n}&{x = 2m,y = 2n} \\ {m + n + 1}&{x = 2m + 1,y = 2n} \\ {m + n + 1}&{x = 2m,y = 2n + 1} \\ {m + n + 1}&{x = 2m + 1,y = 2n + 1} \end{matrix}} \right. \\ &= \left\lfloor {x/2} \right\rfloor + \left\lfloor {y/2} \right\rfloor + \left\lceil {\left( {x\bmod 2 + y\bmod 2} \right)/2} \right\rceil \\ \end{aligned}$$
其中 $m,n$ 均为整数.
借用上面的公式可以将 $\left\lfloor {\left( {x + y} \right)/2} \right\rfloor$ 转化为如下的 C/C++ 代码 (据说这段代码还被申请了专利):
(x >> 1) + (y >> 1) + (x & y & 1);
可以将 $\left\lceil {\left( {x + y} \right)/2} \right\rceil$ 转化为如下的 C/C++ 代码:
(x >> 1) + (y >> 1) + ((x | y) & 1);
这两段代码都不会发生数值溢出.
方式二
设 x 和 y 只能取 0 和 1 值, 则:
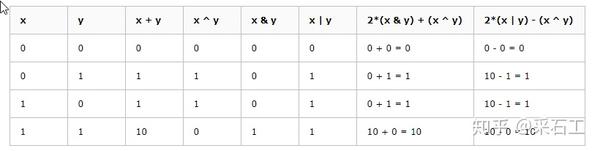
注意上表中的 10 是二进制下的 10, 即十进制下的 2, & 是逻辑与操作, | 是逻辑或运算, ^ 是逻辑异或操作.
由上表可见 x + y = 2*(x & y) + (x ^ y) = 2*(x | y) - (x ^ y) .
无符号整型
对于无符号整型, 设 $x = \sum\nolimits_{i = 0}^{n - 1} {{u_i}{2^i}}$ 和 $y = \sum\nolimits_{i = 0}^{n - 1} {{v_i}{2^i}}$ , 其中 $u_i,v_i\in\left\{ 0, 1 \right\}$ .
$$\begin{aligned} x + y &= \sum\nolimits_{i = 0}^{n - 1} {{u_i}{2^i}} + \sum\nolimits_{i = 0}^{n - 1} {{v_i}{2^i}} \\ &= \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i} + {v_i}} \right){2^i}} \\ &= \sum\nolimits_{i = 0}^{n - 1} {\left( {2 \times \left( {{u_i}\& {v_i}} \right) + \left( {{u_i} \wedge {v_i}}\right)} \right){2^i}} \\ &= 2\sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}\& {v_i}} \right){2^i}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i} \wedge{v_i}} \right){2^i}} \\ \end{aligned}$$
$$\begin{aligned} \left\lfloor {\left( {x + y} \right)/2} \right\rfloor &=\left\lfloor {\sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}\& {v_i}} \right){2^i}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}} } \right\rfloor \\ &= \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}\& {v_i}} \right){2^i}} + \sum\nolimits_{i = 1}^{n - 1} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}} \\ \end{aligned}$$
上式用 C/C++语言可以表示为:
(x & y) + ((x ^ y) >> 1);
$$\begin{aligned} x + y &= \sum\nolimits_{i = 0}^{n - 1} {{u_i}{2^i}} + \sum\nolimits_{i = 0}^{n - 1} {{v_i}{2^i}} \\ &= \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i} + {v_i}} \right){2^i}} \\ &= \sum\nolimits_{i = 0}^{n - 1} {\left( {2 \times \left( {{u_i}|{v_i}} \right) - \left( {{u_i} \wedge {v_i}}\right)} \right){2^i}} \\ &= 2\sum\nolimits_{i = 0}^{n - 1} {\left({{u_i}|{v_i}} \right){2^i}} - \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}\wedge {v_i}} \right){2^i}} \\ \end{aligned}$$
$$\begin{aligned} \left\lceil {\left( {x + y} \right)/2} \right\rceil &= \left\lceil {\sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}|{v_i}} \right){2^i}} - \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}} } \right\rceil \\ &= \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}|{v_i}} \right){2^i}} - \sum\nolimits_{i = 1}^{n - 1} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}} \\ \end{aligned}$$
上式用 C/C++ 语言可以表示为:
(x | y) - ((x ^ y) >> 1);
有符号整型
对于有符号整型, 设 $x = - {u_{n - 1}}{2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {{u_i}{2^i}}$ 和 $y = - {v_{n - 1}}{2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {{v_i}{2^i}}$ (这里采用的是符号数的 two's-complement 编码表示), 其中 $u_i,v_i\in\left\{0, 1 \right\}$ .
$$\begin{aligned} x + y &= - {u_{n - 1}}{2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {{u_i}{2^i}} - {v_{n - 1}}{2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {{v_i}{2^i}} \\ &= - \left( {{u_{n - 1}} + {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {\left( {{u_i} + {v_i}} \right){2^i}} \\ &= - \left( {2 \times \left( {{u_{n - 1}}\& {v_{n - 1}}} \right) + \left( {{u_{n - 1}} \wedge {v_{n - 1}}} \right)} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {\left( {2 \times \left( {{u_i}\& {v_i}} \right) + \left( {{u_i} \wedge{v_i}} \right)} \right){2^i}} \\ &= 2\left( { - \left( {{u_{n - 1}}\& {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}\& {v_i}} \right){2^i}} } \right) + \left( { - \left( {{u_{n - 1}} \wedge {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {\left( {{u_i} \wedge {v_i}} \right){2^i}} } \right) \\ \end{aligned}$$
$$\begin{aligned} \left\lfloor {\left( {x + y} \right)/2} \right\rfloor &= \left\lfloor {\left( { - \left( {{u_{n - 1}}\& {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}\& {v_i}} \right){2^i}} } \right) + \left( { - \left( {{u_{n - 1}} \wedge {v_{n - 1}}} \right){2^{n - 2}} + \sum\nolimits_{i = 0}^{n - 2} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}} } \right)} \right\rfloor \\ &= \left( { - \left( {{u_{n - 1}}\& {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}\& {v_i}} \right){2^i}} } \right) + \left( { - \left( {{u_{n - 1}} \wedge {v_{n - 1}}} \right){2^{n - 2}} + \sum\nolimits_{i = 1}^{n - 2} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}} } \right) \\ &= \left( { - \left( {{u_{n - 1}}\& {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}\& {v_i}} \right){2^i}} } \right) + \left( { - \left( {{u_{n - 1}} \wedge {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 1}^{n - 1} {\left({{u_i} \wedge {v_i}} \right){2^{i - 1}}} } \right) \\ \end{aligned}$$
上式用 C/C++ 语言可以表示为:
(x & y) + ((x ^ y) >> 1);
$$\begin{aligned} x + y &= - {u_{n - 1}}{2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {{u_i}{2^i}} - {v_{n - 1}}{2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {{v_i}{2^i}} \\ &= - \left( {{u_{n - 1}} + {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {\left( {{u_i} + {v_i}} \right){2^i}} \\ &= - \left( {2 \times \left( {{u_{n - 1}}|{v_{n - 1}}} \right) - \left( {{u_{n - 1}} \wedge {v_{n - 1}}} \right)} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {\left( {2 \times \left( {{u_i}|{v_i}} \right) - \left( {{u_i} \wedge {v_i}} \right)} \right){2^i}} \\ &= 2\left( { - \left( {{u_{n - 1}}|{v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}|{v_i}}\right){2^i}} } \right) - \left( { - \left( {{u_{n - 1}} \wedge {v_{n - 1}}}\right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 2} {\left( {{u_i} \wedge{v_i}} \right){2^i}} } \right) \\ \end{aligned}$$
$$\begin{aligned} \left\lceil {\left( {x + y} \right)/2} \right\rceil &= \left\lceil {\left( { - \left( {{u_{n - 1}}|{v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}|{v_i}} \right){2^i}} } \right) - \left( { - \left( {{u_{n - 1}} \wedge {v_{n - 1}}} \right){2^{n - 2}} + \sum\nolimits_{i = 0}^{n - 2} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}}} \right)} \right\rceil \\ &= \left( { - \left( {{u_{n - 1}}|{v_{n - 1}}}\right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 1} {\left( {{u_i}|{v_i}}\right){2^i}} } \right) - \left( { - \left( {{u_{n - 1}} \wedge {v_{n - 1}}}\right){2^{n - 2}} + \sum\nolimits_{i = 1}^{n - 2} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}} } \right) \\ &= \left( { - \left( {{u_{n - 1}}|{v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 0}^{n - 1} {\left({{u_i}|{v_i}} \right){2^i}} } \right) - \left( { - \left( {{u_{n - 1}} \wedge {v_{n - 1}}} \right){2^{n - 1}} + \sum\nolimits_{i = 1}^{n - 1} {\left( {{u_i} \wedge {v_i}} \right){2^{i - 1}}} } \right) \\ \end{aligned}$$
上式用 C/C++ 语言可以表示为:
(x | y) - ((x ^ y) >> 1);
综合
综合上面的分析, 可见对于有符号整型和无符号整型,
$\left\lfloor {\left( {x + y} \right)/2} \right\rfloor$ 都可以用 C/C++ 语言表示为:
(x & y) + ((x ^ y) >> 1);
$\left\lceil {\left( {x + y} \right)/2} \right\rceil$ 都可以用 C/C++ 语言表示为:
(x | y) - ((x ^ y) >> 1);
参考
- https://stackoverflow.com/questions/24920503/what-is-the-right-way-to-find-the-average-of-two-values
- https://stackoverflow.com/questions/3816446/how-can-i-safely-average-two-unsigned-ints-in-c
更新记录
- 20200529, 发布
版权声明
版权声明: 自由分享, 保持署名-非商业用途-非衍生, 知识共享3.0协议.
如果你对本文有疑问或建议, 欢迎留言! 转载请保留版权声明!